Tabla ANOVA en Excel: cómo crearla e interpretarla

En el siguiente artículo conocerás todo lo que necesitas saber sobre una tabla ANOVA, sus elementos y su aplicación con uno y dos factores.

Información clave

Para comparar promedios de distintos grupos de datos usamos una tabla de análisis de varianza: ANOVA (por su nombre en inglés, Analysis of Variance). Esta tabla contiene los elementos que analizan la variación de los datos y nos sirve para comparar si dos o más grupos son estadísticamente distintos o no.

Lo básico sobre BUSCAR en Excel

Finalidad: El objetivo de una tabla ANOVA es testear si dos o más grupos son estadísticamente iguales o son distintos entre sí.

Hipótesis inicial: También conocida como “hipótesis nula”. Es creencia inicial que tenemos sobre los grupos que tenemos. En estadística esta hipótesis es que los promedios de todos los grupos serán estadísticamente iguales.

Test F: Test que hace la tabla ANOVA para verificar si se cumple la hipótesis inicial, es decir, si los promedios de los grupos son iguales o no. Si el valor de nuestro “valor F” es mayor a un valor crítico vamos a decir que la hipótesis inicial no se cumple, es decir, los promedios de los grupos son estadísticamente distintos.

Instalar el paquete de análisis de datos

Antes de poder empezar con el análisis de una tabla ANOVA en Excel debemos instalar el paquete de análisis de datos para poder crear un tabla ANOVA.

Paso 1: En la barra de herramientas, hacemos click en “Archivo” y luego en “Opciones” (en la esquina inferior izquierda). 

Paso 2: En la nueva ventana de opciones, debemos seleccionar “Complementos”. En la sección “Administrar”, seleccionamos “Complementos de Excel” y luego hacemos click en “Ir”.

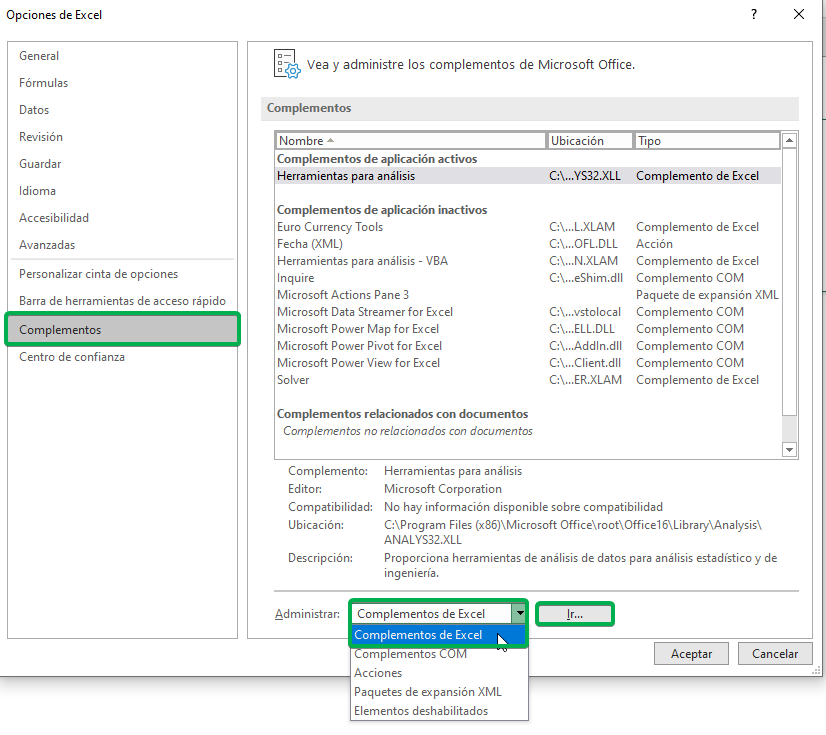
Paso 3: Aparecerá una nueva ventana, en la que debemos verificar “Herramientas para análisis” y luego hacer click en “Aceptar”.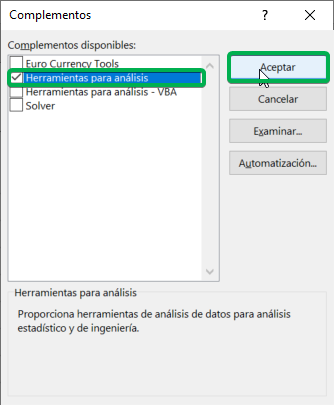

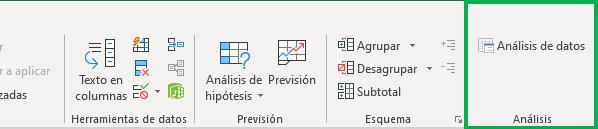
Si vamos a la pestaña “Datos” de la barra de herramientas, veremos que se ha agregado una nueva sección llamada “Análisis”, la que incluye la herramienta de “Análisis de datos”. 

Tip Ninja: Para instalar este paquete en Mac debemos ir a la barra de herramientas, hacemos click en “Herramientas” y luego en “Complementos de Excel”. Luego, aparecerá una nueva ventana, en la que debemos verificar “Herramientas para análisis” y luego hacemos click en “Aceptar”. Con este complemento puedes hacer regresiones lineales, obtener coeficientes de correlación, hacer pruebas t y usar muchas otras herramientas de análisis de datos.

ANOVA de un factor

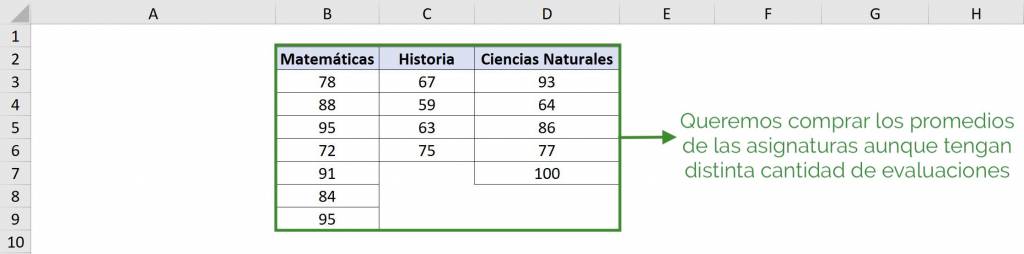
Para entender qué es una tabla ANOVA de un factor veremos un ejemplo aplicado. En este caso, que tenemos las calificaciones de un alumno para tres distintas asignaturas: Matemáticas, Historia y Ciencias Naturales.

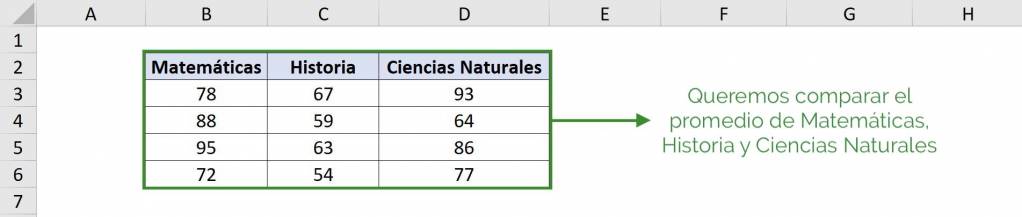
Nuestro objetivo es saber si es que el promedio que tiene en cada asignatura es estadísticamente igual a las otras asignaturas. Esto es, ver si el promedio en Matemáticas es igual el promedio en Historia y el Ciencias Naturales. 

Para esto debemos:

1. Vamos a la pestaña “Datos” y apretamos en “Análisis de datos”.
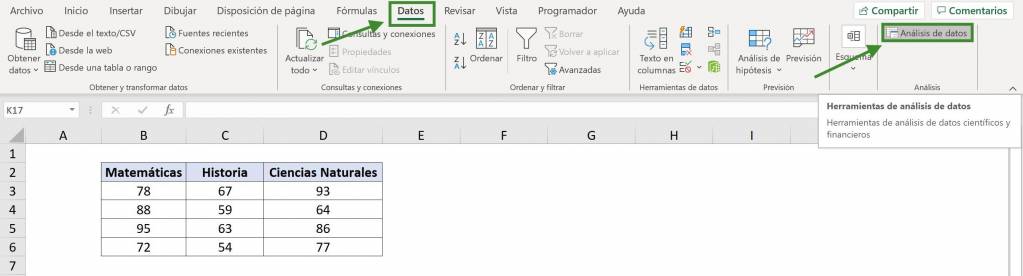
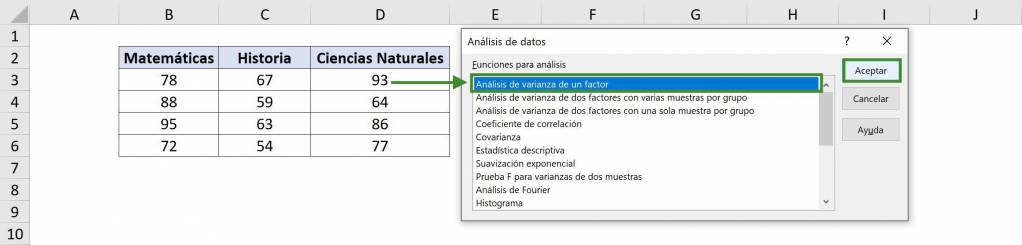
2. En la ventana que se abre debemos seleccionar “Análisis de Varianza de un factor”.
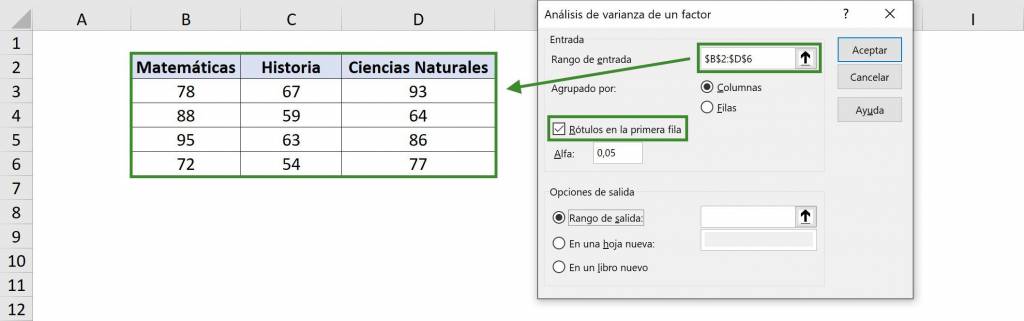
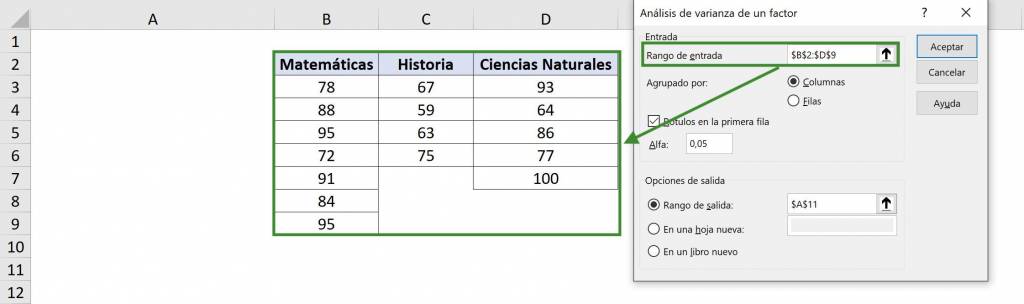
3. En “Rango de entrada” seleccionamos nuestra tabla con datos. En este caso es $B$2:$D$6 y como incluimos los títulos debemos seleccionar la opción “Rótulos en la primera fila”.
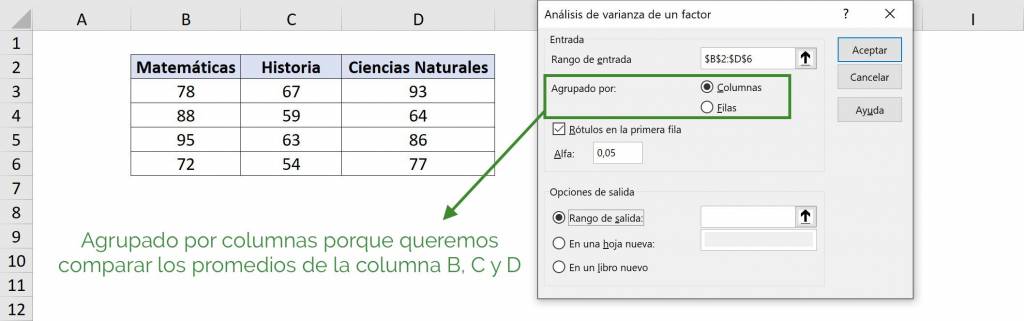
4. En la sección de “Agrupado por”, debemos elegir el sentido de cada grupo: como cada grupo es una columna distinta seleccionamos “Columnas”. Esto es porque queremos comparar una columna con otra.
5. Para el valor de “Alfa” en general se usa 5%, lo que significa que se estima con una confianza del 95%. Si quisiéramos ser más estrictos podemos elegir un valor menor, como 1% (para tener un 99% de confianza). Puedes profundizar en este concepto en este artículo.
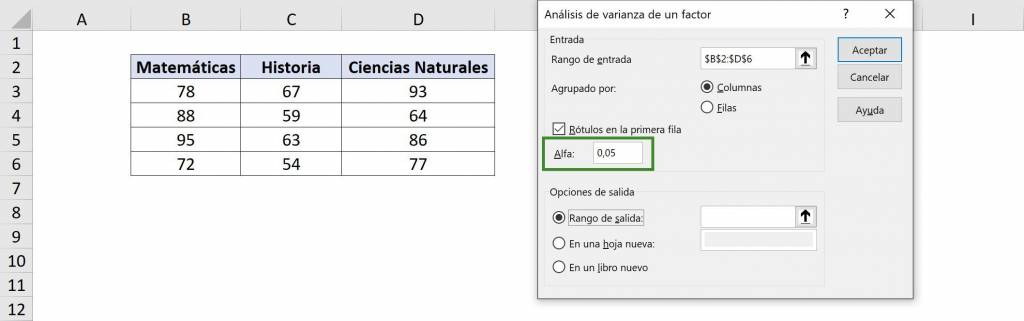
6. En “Rango de salida” debemos elegir la celda en donde comenzará la información del análisis de varianza, es decir, la esquina superior izquierda. En este caso seleccionaremos $A$8. Finalmente hacemos click en “Aceptar”.

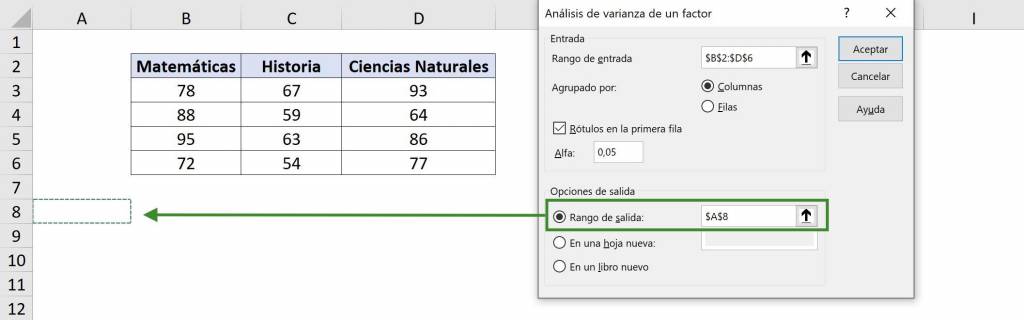
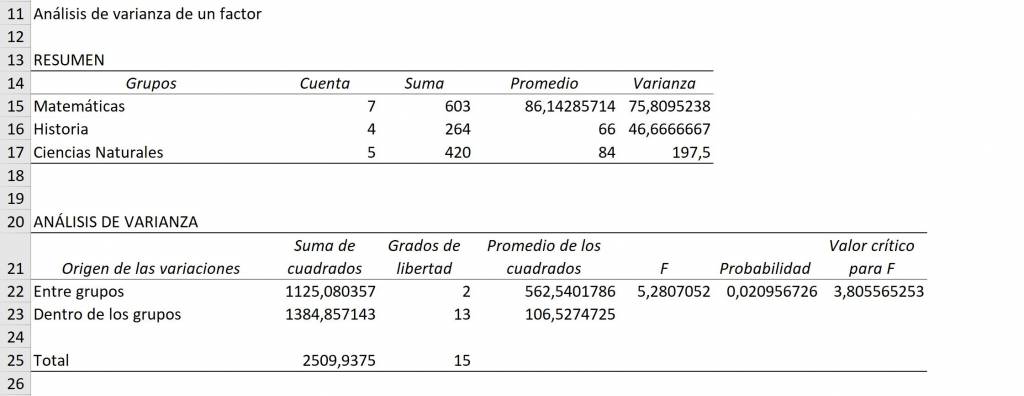
Así, obtenemos como resultado una tabla de resumen de observaciones, promedio y varianza de cada grupo y una tabla ANOVA.

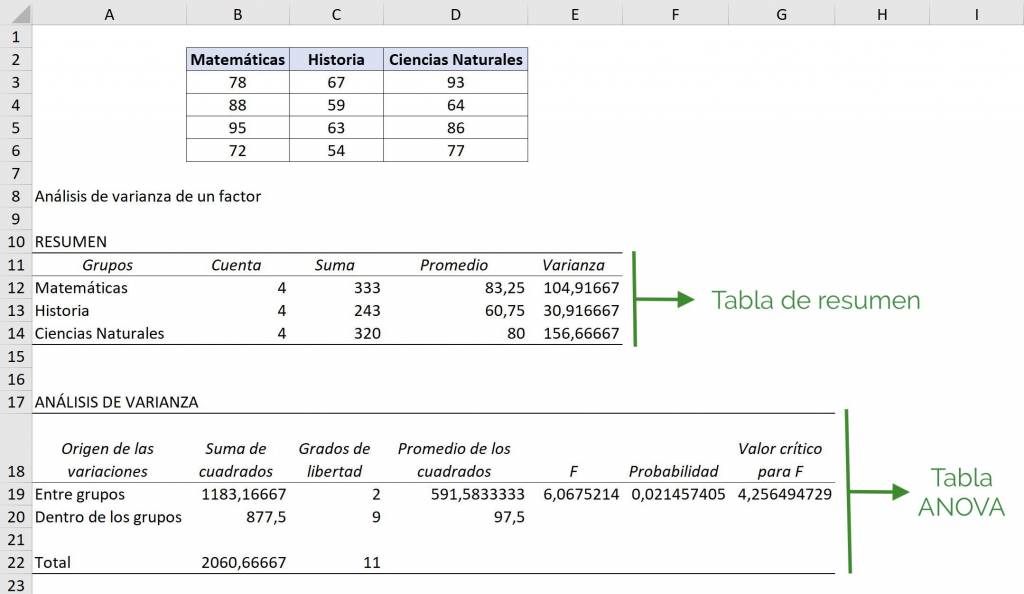
Tip Ninja: Como podemos ver, los resultados son parte de la planilla y se van a sobreescribir sobre lo que haya anteriormente. Por esto es importante que nos preocupemos de tener el espacio suficiente en la planilla para no perder datos.

Ahora, al analizar la tabla ANOVA nuestro objetivo es ver si se cumple nuestra hipótesis inicial: si el valor F es mayor al valor crítico de F, vamos a rechazar la hipótesis de que los promedios de los grupos son iguales. Es decir, si F es mayor al valor crítico, vamos a decir al menos uno de los promedios de estos grupos es estadísticamente distinto.

Para ver esto en la tabla ANOVA misma vamos a la fila que dice “Entre grupos” y vemos que el valor F es 6.06, mientras que el valor crítico de F es 4.25. Como esto significa que los promedios en Matemáticas, Historia y Ciencias Naturales no son todos iguales entre sí, es decir, al menos un promedio es distinto.

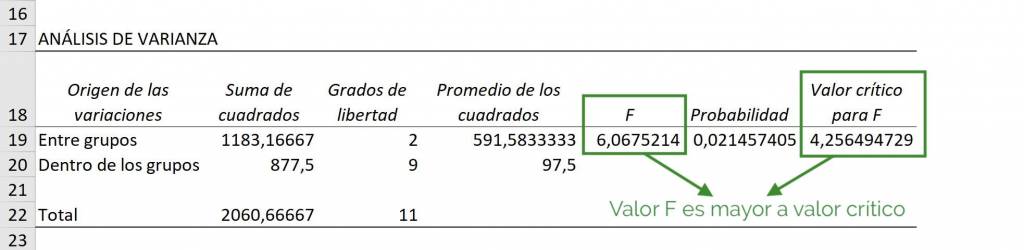
Tip Ninja: El valor crítico para F va a disminuir a medida que tengamos más datos de cada grupo. Esto significa que mientras más datos tengamos más seguros podemos estar de una diferencia estadística.

Sin embargo, un análisis tipo ANOVA no nos dice qué grupo (o grupos) es (son) el distinto(s) ni si es mayor o menor que el resto. Para esto debemos hacer un test t para ver cada par de grupos si son iguales o distintos entre sí.

Tip Ninja: No necesitamos tener la misma cantidad de datos para cada grupo para hacer la comparación de promedios con una tabla ANOVA. Por ejemplo, en este caso seleccionamos $B$2:$D$9 dejando en blanco aquellas celdas que no tienen datos.

Obteniendo el siguiente resultado:

ANOVA de dos factores con una muestra por grupo

Una tabla ANOVA de dos factores consiste en que dos tipos de grupos y queremos estudiar si hay diferencias entre grupos para ambos tipos. Esto se entiende mejor con un ejemplo: pensemos en un curso que tiene varios alumnos y que se han rendido varias pruebas.

En este caso queremos ver si los promedios de los alumnos son estadísticamente iguales entre ellos, y además, queremos ver si los promedios de las pruebas son estadísticamente iguales entre ellas. Por esto es una ANOVA de dos factores: queremos estudiar los promedios de los alumnos y de las pruebas.

De esta manera seguimos pasos similares a los para una tabla ANOVA de un factor:

1. Vamos a la pestaña “Datos” y apretamos en “Análisis de datos”.
2. En la ventana que se abre debemos seleccionar “Análisis de Varianza de dos factores con una muestra por grupo”.
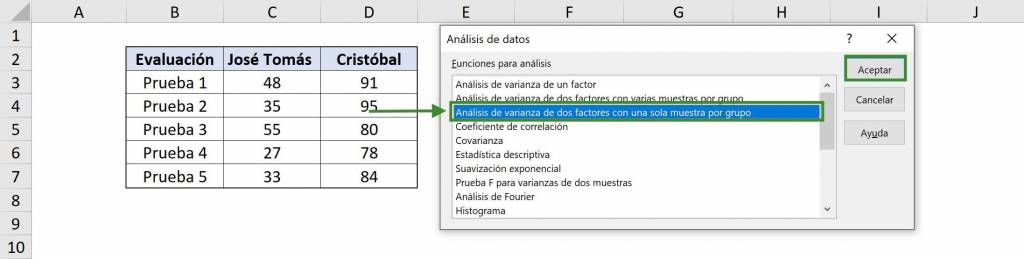
3. En “Rango de entrada” seleccionamos nuestra tabla con datos. En este caso es $B$2:$D$7 y como incluimos los títulos debemos seleccionar la opción “Rótulos”.
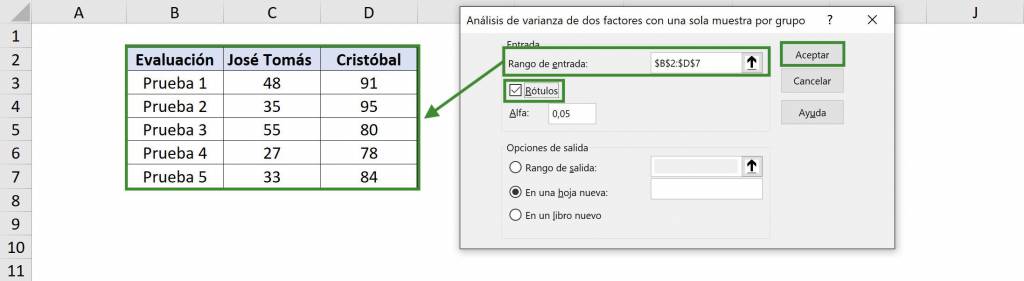
4. Para el valor de “Alfa” en general se usa 5%, lo que significa que se estima con una confianza del 95%.
5. En “Rango de salida” debemos elegir la celda en donde comenzará la información del análisis de varianza, es decir, la esquina superior izquierda. En este caso seleccionaremos $A$9. Finalmente hacemos click en “Aceptar”.

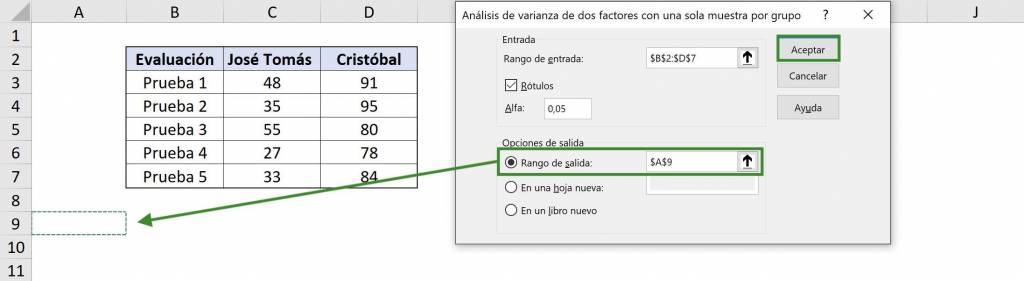
Así, obtenemos como resultado una tabla de resumen de observaciones, promedio y varianza de cada grupo de cada tipo, es decir, para cada prueba para cada alumno.

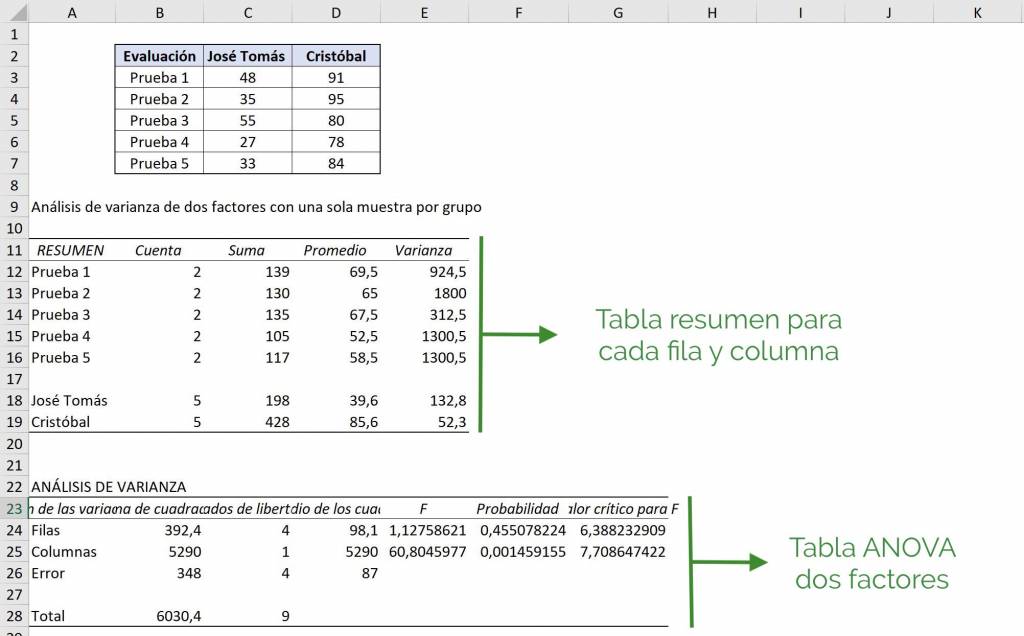Ahora, al analizar la tabla ANOVA de dos factores tenemos dos aspectos que queremos estudiar: la diferencia de promedios entre pruebas y entre alumnos. Al ver la sección “Filas” se está testeando entre filas, es decir, está comparando si las pruebas tienen los mismos promedios o no. Como vemos, el valor F es 1.12 es menor al valor crítico de F (6.38) vemos que se acepta la hipótesis inicial en que los promedios de las pruebas son estadísticamente los mismos.

Luego, para la sección de “Columnas” se están comparando entre columnas, es decir, está comparando los promedios de José Tomás y Cristóbal. En la tabla ANOVA vemos que el valor F es 60.80 que es mucho mayor al valor crítico para F que es 7.70. De esta manera rechazamos que tengan el mismo promedio estadísticamente.

ANOVA de dos factores con varias muestras por grupo

Una tabla ANOVA de dos factores con varias muestras por grupo, al igual que el caso anterior, consiste en que dos tipos de grupos y queremos estudiar si hay diferencias entre grupos para ambos tipos. Sin embargo, en este caso tenemos varios datos para cada grupo. Veamos un ejemplo: pensemos que tenemos dos colegios y dos asignaturas y que para cada asignatura dentro de un colegio tenemos varias calificaciones.  

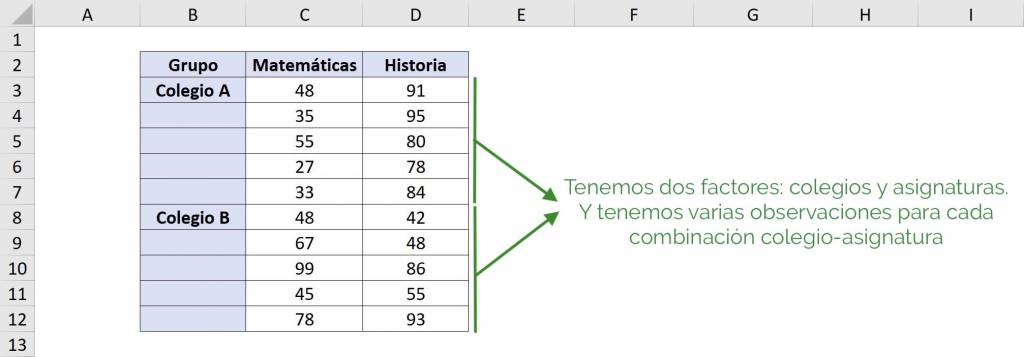
En este caso queremos ver si los promedios de cada colegio son estadísticamente iguales entre ellos, y además, queremos ver si los promedios de las asignaturas son estadísticamente iguales entre ellas. Por esto es una ANOVA de dos factores: queremos estudiar los promedios de cada colegio y de cada asignatura. Finalmente, al ser de varias muestras por grupos, podemos estudiar si las interaccións “colegio-asignatura” son iguales entre ellas.

De esta manera seguimos pasos similares a los para una tabla ANOVA en Excel de un factor:

1. Vamos a la pestaña “Datos” y apretamos en “Análisis de datos”.
2. En la ventana que se abre debemos seleccionar “Análisis de Varianza de dos factores con varias muestras por grupo”.
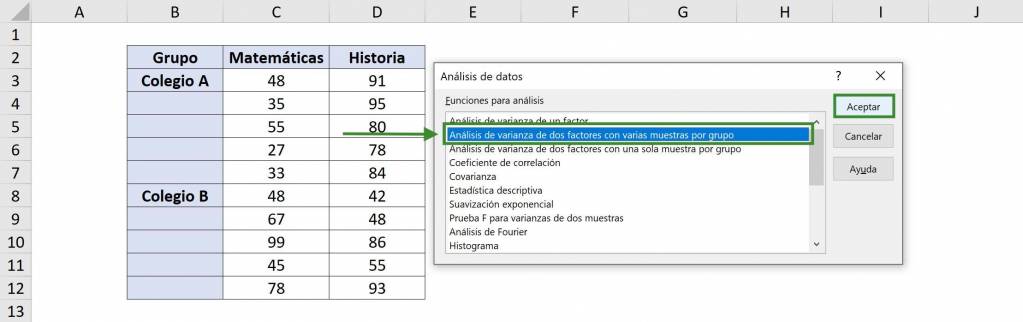
3. En “Rango de entrada” seleccionamos nuestra tabla con datos. En este caso es $B$2:$D$12, incluyendo los títulos de la tabla.
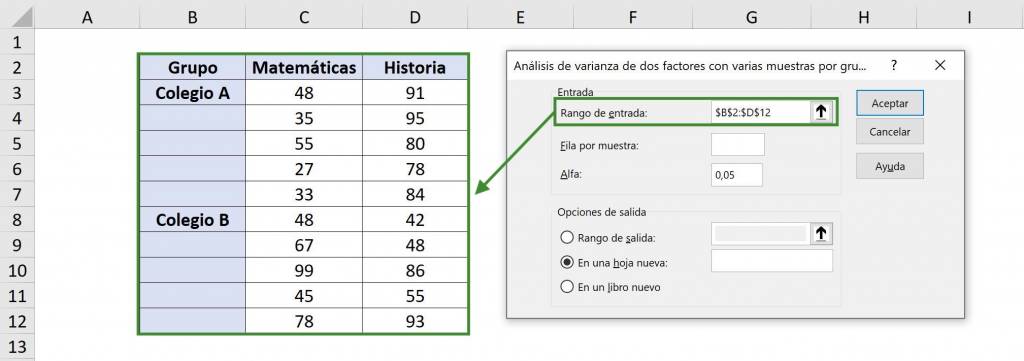
4. En “Fila por muestra” debemos poner cuántas observaciones tenemos para cada grupo. En este caso, tenemos 5 calificaciones para cada colegio, dada una asignatura.
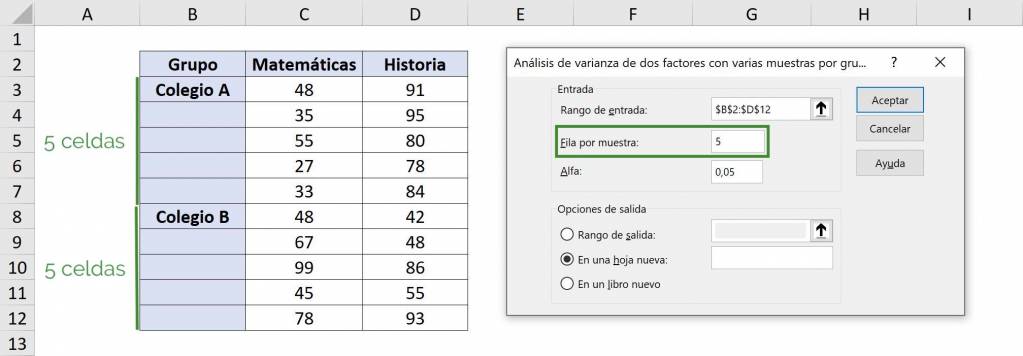
5. Para el valor de “Alfa” en general se usa 5%, lo que significa que se estima con una confianza del 95%.
6. En “Rango de salida” debemos elegir la celda en donde comenzará la información del análisis de varianza, es decir, la esquina superior izquierda. En este caso seleccionaremos $F$12. Finalmente hacemos click en “Aceptar”.

Finalmente, obtenemos:

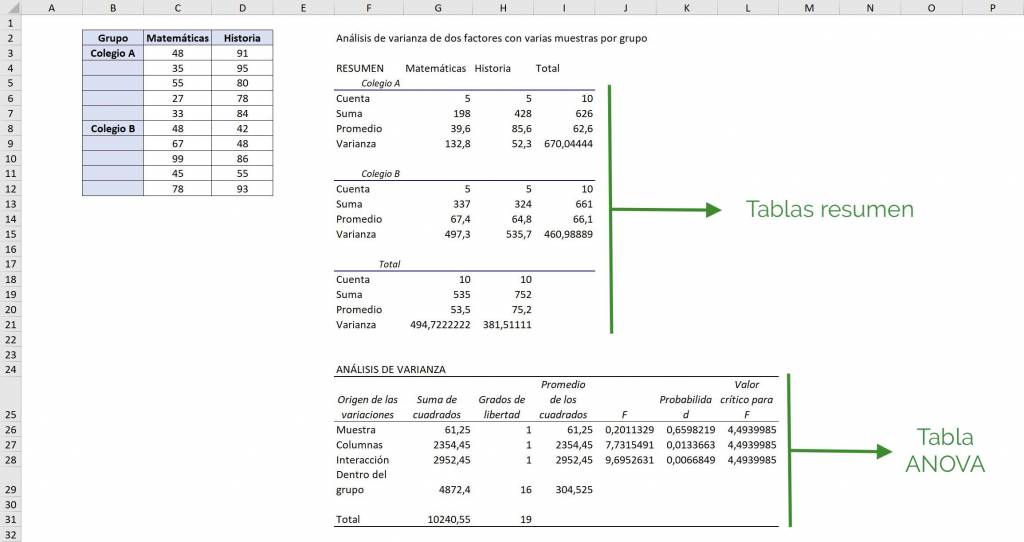Así, obtenemos una tabla resumen para el Colegio A, para el Colegio B y para ambos como un conjunto haciendo un análisis para cada asignatura.

Luego, en la tabla ANOVA vemos que en la sección “Muestra” se comparan columnas entre sí, por lo que compara Matemáticas e Historia y vemos que no rechazamos la hipótesis inicial (0.20<4.49), por lo que los promedios son iguales estadísticamente. En cuanto a la sección “Columnas” compara el promedio para el Colegio A con el Colegio B y vemos que sí hay una diferencia entre colegios (7.73>4.49).

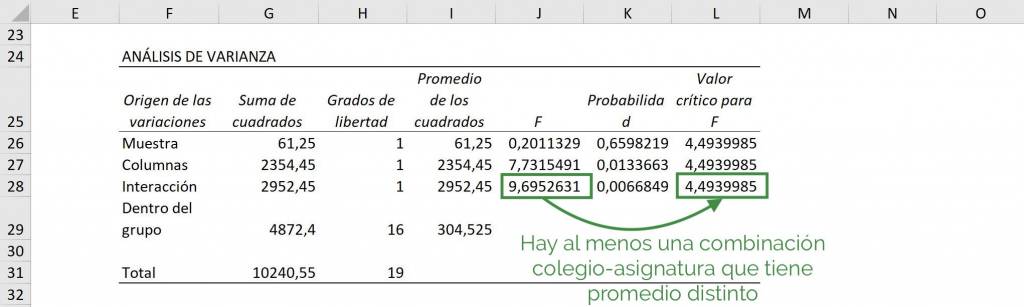
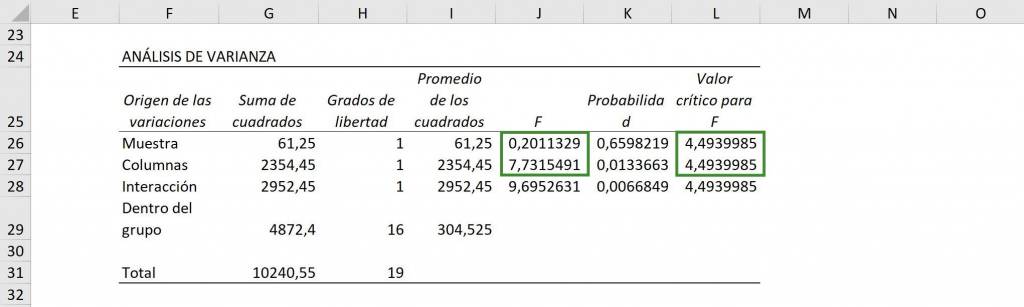Finalmente, vemos la interacción: ¿es igual el Colegio A en Matemáticas, el Colegio A en Historia, el Colegio B en Matemáticas y el Colegio B en Historia? Al ver que el valor de F (9.69) es mayor al valor crítico de F (9.69>4.49), vemos que hay al menos un grupo que es distinto.

Preguntas Frecuentes