Desviación estándar en Excel: Cómo calcularla fácilmente

Información clave

La desviación estándar es una medida usada para cuantificar la dispersión que hay en una muestra de datos. Según usemos una muestra o población debemos usar diferentes funciones de Excel, además de tomar en cuenta si consideramos texto y valores lógicos. Excel tomará los argumentos para calcular la desviación estándar o típica según la fórmula que decidamos.

¿Qué es la desviación estándar?

La desviación estándar -también conocida como desviación típica- es una medida usada para cuantificar la dispersión que hay en un conjunto de datos. Esta variación se calcula con respecto al promedio (media) del conjunto. Así, una desviación estándar baja significa que la mayor parte de los números se agrupa cerca de su media, mientras que una desviación estándar alta significa que se extienden sobre un rango más grande.

Podemos ver en el siguiente ejemplo, en el que usamos Excel para calcular el promedio y la desviación estándar, que ambos grupos tienen el mismo promedio. Sin embargo, tienen diferentes desviaciones estándar:

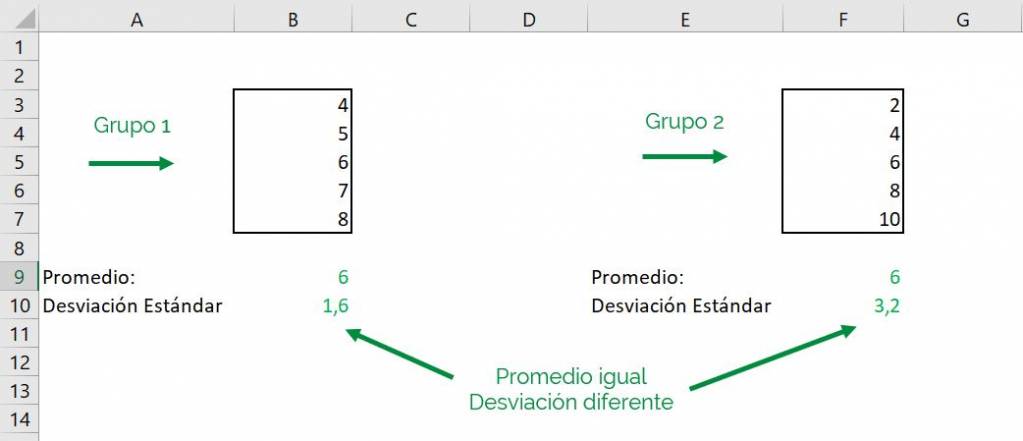
Vemos que esto se debe a que los números del grupo 2 se alejan más del promedio del grupo, que corresponde a 6. Por lo tanto, decimos que este grupo tiene mayor desviación estándar.

Agreguemos ahora un tercer grupo al ejemplo:

Podemos ver que el tercer grupo mantiene el promedio de los otros 2, pero con una desviación estándar de 0. Esto se debe a que todos los números son iguales, por lo que el promedio es el mismo y así la dispersión respecto a ese número es nula.

Calculando la desviación estándar en Excel

Dependiendo de si calculamos la desviación estándar de una muestra o una población debemos usar funciones diferentes. Para el caso de una muestra, es decir, un grupo dentro de una población, debemos usar DESVEST M y para el caso de la población total debemos usar DESVEST P.

Tip Ninja: La “M” al final del nombre DESVEST M hace referencia a que se usa en muestras, mientras que la “P” al final de DESVEST P es porque se usa en poblaciones.

Esto significa que si estamos calculado la desviación estándar de los sueldos de toda una empresa, usamos DESVEST P, ya que corresponde a toda la población. Por otro lado, si tenemos solo un grupo más pequeño de estos sueldos, utilizamos DESVEST M.

Podemos ver en el siguiente ejemplo que el cálculo de la desviación estándar con estas 2 funciones nos entrega distintos resultados:

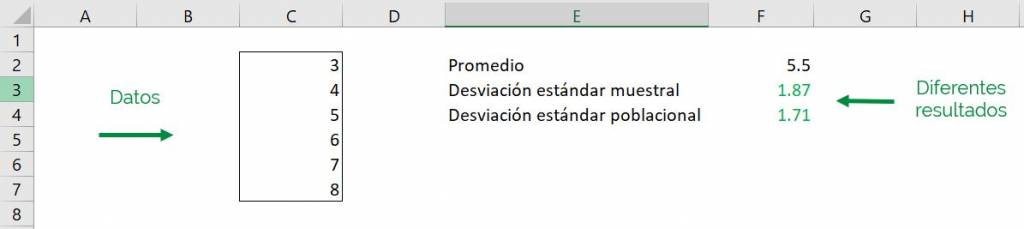
Tip Ninja:  A medida que aumente el número de datos usados en el cálculo de la desviación estándar en Excel, la diferencia entre estas dos funciones será menor.

Si estás interesado en aprender sobre las diferencias entre usar una muestra y una población ve este artículo.

Excel DESVEST M Y DESVEST P: Desviación para muestras y poblaciones

Lo básico

Características: Solo el primer valor es obligatorio, el resto es opcional. Los argumentos numéricos pueden ser números, filas, columnas o matrices. Las funciones omiten casillas en blanco o que incluyan texto.

Sintáxis:

=DESVEST.M(número1, [número2],…)

=DESVEST.P(número1, [número2],…)

Argumentos:

• número1  = Primer argumento numérico.
• número2, número3, …  = El resto de los argumentos numéricos. Pueden ser hasta 255.

Usando DESVEST M y DESVEST P

Dado que las funciones DESVEST M y DESVEST P funcionan igual y solo se diferencian en cuando se deben usar, para los siguientes ejemplos usaremos DESVEST M. Sin embargo, recordemos que todo es aplicable a DESVEST P

Como ya vimos en la sintaxis de las funciones, para calcular la desviación estándar en Excel solo se necesitan argumentos numéricos. Sin embargo, cada uno de estos argumentos pueden ser números, filas, columnas o matrices.

En el siguiente ejemplo podemos ver que cada uno de los números usados para el cálculo de la desviación estándar se selecciona como un argumento diferente:

Tip Ninja:  Mantén apretado el botón “Control” o “CTRL” (“Comand” o “Cmd” si es que estás usando un Mac) para seleccionar nuevos datos sin que se te borren selecciones anteriores. Esto es muy útil para seleccionar grandes números de datos que no necesariamente están unidos.

Aquí la celda B3 corresponde al primer argumento (5), la celda C3 al segundo y así sucesivamente. Esto nos dará como resultado lo siguiente:

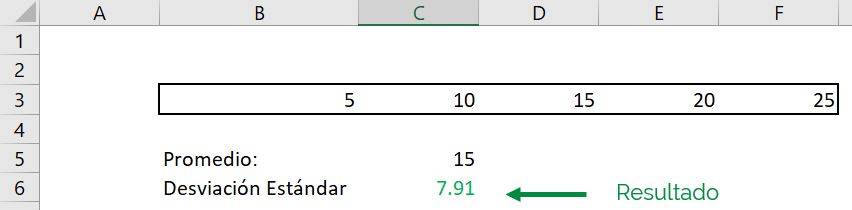
Si es que ahora para calcular la desviación estándar en Excel seleccionamos toda la línea como un solo argumento, obtendremos el mismo resultado:

Como podemos ver, obtenemos el mismo 7,91 del primer ejemplo:

Otro punto importante a la hora de calcular la desviación estándar en Excel es que las funciones DESVEST M y DESVEST P omiten celdas en blanco y celdas que contengan texto a la hora de sacar la desviación estándar.

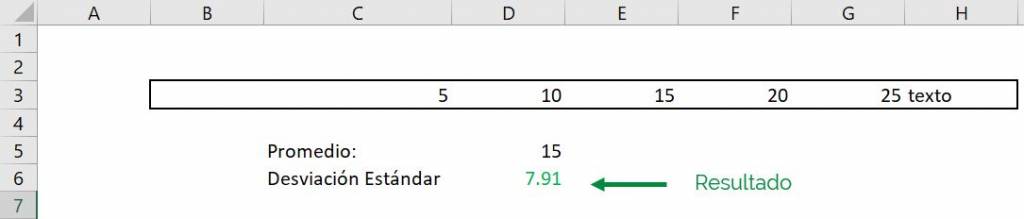
En el siguiente ejemplo agregamos al rango usado para el cálculo de la desviación típica un espacio en blanco y una casilla que dice “texto”

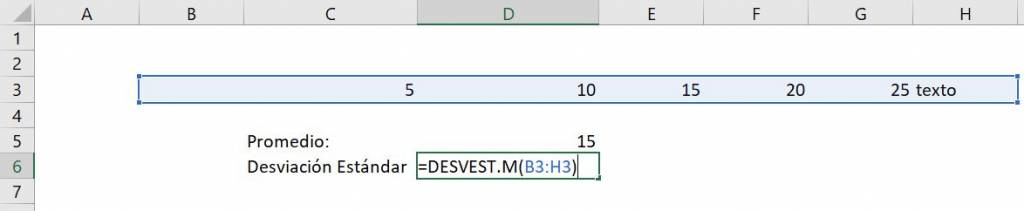
Vemos que igual Excel nos entrega como resultado la misma desviación estándar que antes:

Diferencia con las funciones de Excel DESVEST y DESVESTP

Nos podremos estar preguntando cuál es la diferencia entre las funciones de Excel DESVEST Y DESVEST M. Ambas funciones hacen exactamente lo mismo: entregar la desviación estándar (o desviación típica) muestral en Excel.

De la misma forma, DESVEST P hace lo mismo que DESVESTP,entregar la desviación estándar poblacional en Excel.

Las funciones DESVEST M y DESVEST P corresponden a versiones actualizadas de DESVEST y DESVESTP respectivamente. Sin embargo, Microsoft decide seguir incluyendo ambas versiones en Excel, para que sean compatibles con versiones anteriores del programa. Sin embargo, recomiendan que a la hora de calcular la desviación estándar en Excel uses DESVEST M Y DESVEST P, ya que tienen un mejor rendimiento y sus nombres reflejan más fielmente para que se usan.

Tal como muestra el ejemplo, obtenemos el mismo resultado usando DESVEST Y DESVEST M:

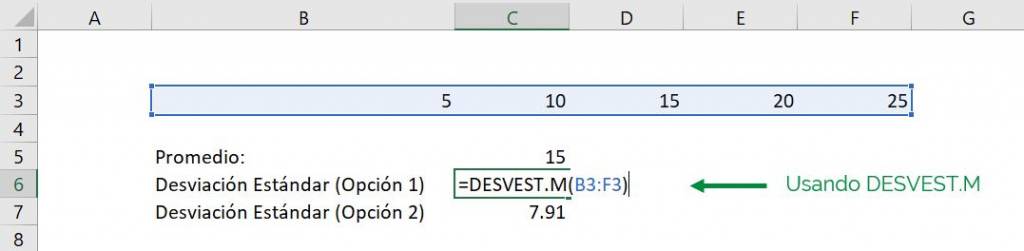
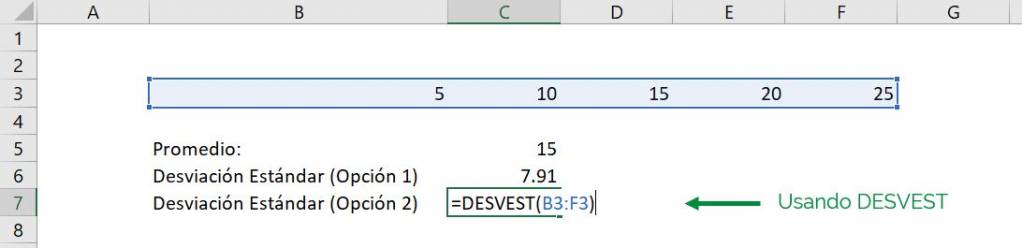
Como vemos, ambas funciones de Excel entregan 7.91 como desviación estándar de la muestra.

Excel DESVESTA y DESVESTPA: Calculando desviación estándar incluyendo texto y valores lógicos

Lo básico

Finalidad: DESVESTA nos permite obtener la desviación estándar de una muestra de datos, pero considerando texto y valores lógicos. DESVESTPA hace lo mismo, pero para una población de datos

Características: Solo el primer valor es obligatorio, el resto es opcional. A diferencia de DESVEST M y DESVEST P, los argumentos no son solo números, sino que también texto y valores lógicos.

Sintaxis:

=DESVESTA (valor1, [valor2],…)

=DESVESTPA (valor1, [valor2],…)

Argumentos:

• valor1 = Primer argumento. Puede ser número, texto o valor lógico.
• valor2, valor3, …  = El resto de los argumentos. Pueden ser hasta 255.

Calculando desviación estándar incluyendo texto con DESVESTA y DESVESTPA

A diferencia de con DESVEST M y DESVEST P, al calcular la desviación estándar con DESVESTA las celdas que tengan texto serán consideradas por la función como celdas con valor 0.

En el siguiente ejemplo, usamos el mismo rango numérico que en el ejemplo de DESVEST M:

Y así obtenemos la misma desviación estándar:

Pero, al incluir ahora una celda que diga “texto” (acá podría ser cualquier palabra):

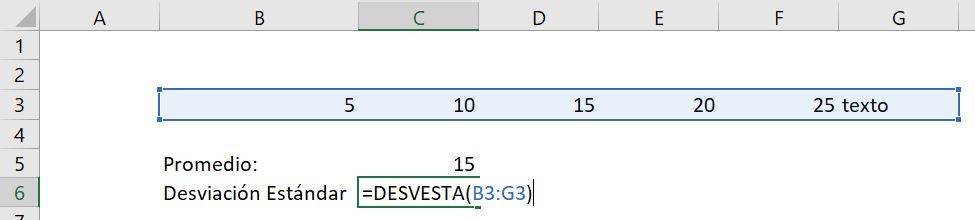
Vemos que Excel ahora entrega una desviación estándar diferente:

Lo que significa que la desviación estándar aumentó de 7.91 a 9.35. Esto ocurre porque la casilla “texto” toma el valor 0, que se encuentra relativamente alejado del promedio de 15, por lo que aumenta la desviación estándar.

Calculando desviación estándar incluyendo valores lógicos con DESVESTA y DESVESTPA

Las funciones DESVESTA y DESVESTPA también toman en cuenta valores lógicos (verdadero o falso) a la hora de calcular la desviación estándar en Excel.

Si es que usamos un “VERDADERO”, Excel lo reconocerá como un 1, mientras que si usamos un “FALSO”, lo reconocerá como un 0.

Si volvemos al ejemplo anterior y reemplazamos la palabra “texto” por “FALSO”:

Obtenemos el mismo resultado que antes, ya que Excel reconoce “FALSO” como 0, al igual que “texto.

Sin embargo, al reemplazar “FALSO” por “VERDADERO”:

La desviación estándar calculada por Excel disminuye a 9.09. Esto tiene sentido porque 1 (“VERDADERO”) está más cerca del promedio (15) que 0 (en el caso de “Falso”).

Resumen de las funciones de Excel para calcular desviación estándar.

Función	Tipo de datos	Considera texto y valores lógicos	Versión actualizada
DESVEST	Muestra	No	No
DESVEST.M	Muestra	No	Sí
DESVESTP	Población	No	No
DESVEST.P	Población	No	Sí
DESVESTA	Muestra	Sí	Sí
DESVESTPA	Población	Sí	Sí

Preguntas Frecuentes