Regresión lineal en Excel: Aprende, calcula, interpreta

Lo básico

¿Qué relación existe entre los años de educación y el salario? ¿Afecta también la experiencia? Un análisis de regresión te permite calcular la relación numérica que existe entre el salario y el conjunto de características que pueden afectarlo, como la educación, la experiencia o el rubro donde trabajas. Puedes aplicar este análisis para cualquier conjunto de variables que desees, ¡incluso las que no son numéricas!

Para lograrlo necesitas tener la suficiente cantidad de información para que la estimación sea confiable. ¿Cuánto es suficiente? La regla de pulgar es 30. Es decir, para el caso anterior, necesitamos mínimo 30 personas para quienes tengamos información de su salario, años de educación, experiencia y rubro donde trabajan. Si tienes más, ¡mejor aún! Le estimación será cada vez más precisa a medida que tengas más datos.

Información clave 

• Variable dependiente: es aquella sobre la cual se quiere medir el efecto. Para el caso anterior, tendremos que la variable dependiente es el salario. 
• Variable(s) independiente: son aquellas que tratan de explicar a la variable dependiente. En el ejemplo, tendríamos a educación, experiencia y rubro como variables independientes. 
• Observaciones: se refiere a la cantidad de datos que va a incorporar la regresión. Cada fila corresponde a una observación. Para el caso del ejemplo, cada observación corresponde a una persona (con su salario, sus años de educación y su experiencia). Esto no necesariamente ocurre así, pues depende del tipo de datos que tengamos. 
• Forma funcional: una regresión lineal se puede expresar matemáticamente como: 
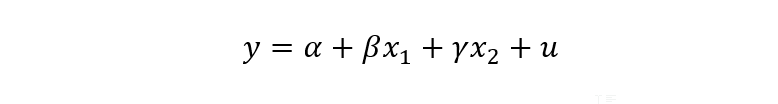
• Que para efectos del ejemplo sería lo mismo que: 

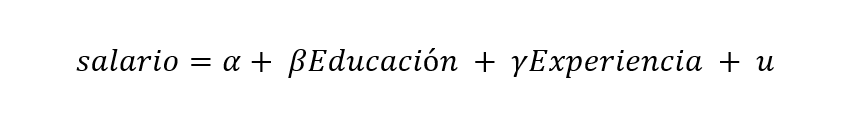
Más adelante veremos en detalle qué significan cada uno de estos elementos. 

Regresión lineal en Excel de manera simple: el caso más fácil

A una regresión con tan solo una variable independiente se le conoce como regresión lineal simple. Para mantenernos con el ejemplo, consideremos que queremos ver la relación entre el salario y la educación. 

Paso 1: Selecciona toda la tabla con información. 

Paso 2: En la pestaña “Insertar”, dirígete a la sección de “Gráficos” y selecciona la primera opción para “Dispersión”.

Aparecerá un gráfico que relaciona los años de educación (en el eje X) con el salario (en el eje Y). 

Tip Ninja: Excel entiende que la columna que está a la derecha de la tabla es aquella que va en el eje X. Asegúrate de que tus columnas estén ordenadas de esta manera para que el gráfico quede como deseas en el primer intento. 

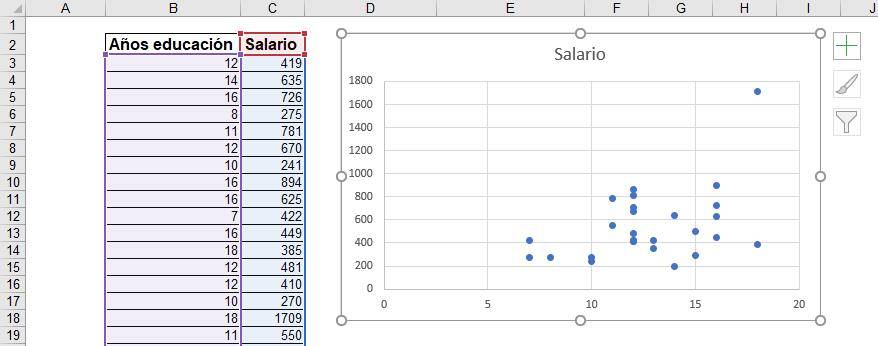
A simple vista podemos ver que la relación es positiva. 

Paso 3: Haz click derecho sobre cualquiera de los puntos del gráfico, y selecciona “Agregar lína de tendencia”. Aparecerá una sección a la derecha de la pantalla con el título “Formato de línea de tendencia”. 

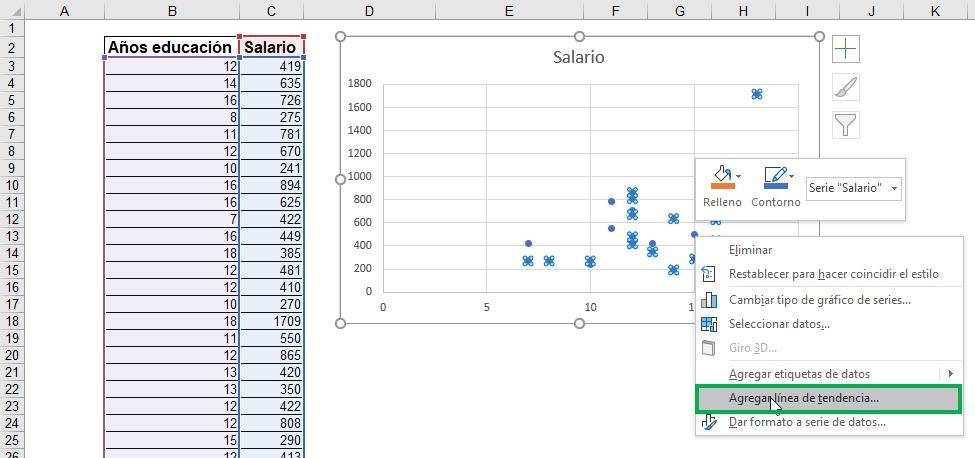
Paso 4: En “Opciones de línea de tendencia”, selecciona “lineal” y luego, al final de la sección, haz click en las casillas de “Presentar ecuación en el gráfico”

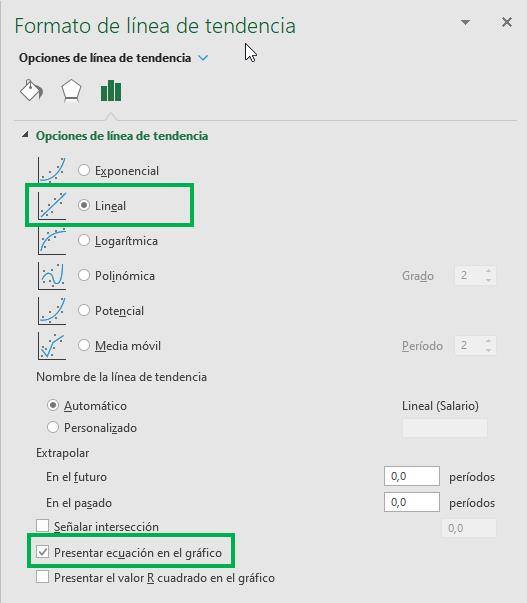
El resultado es el siguiente. 

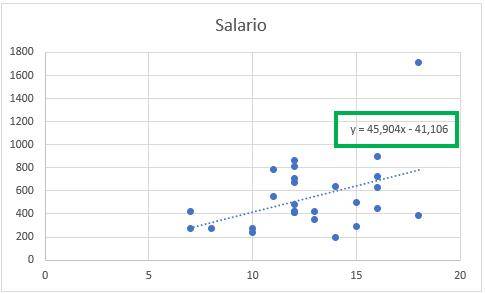
Vemos que ahora el gráfico incluye una línea de tendencia y además la ecuación que da forma a esa línea. La regresión lineal, entonces, es simplemente una línea que trata de ajustar todos los datos lo mejor posible. Esta ecuación indica que por cada año adicional de educación, el salario aumenta en 45,9. Es decir, la “x” de la ecuación representa a la variable educación, mientras que la “y” representa al salario.

Claramente, existe un error en la estimación ya que no todos los puntos se ubican sobre la línea. A esta diferencia se le llama residuo, y veremos cómo se calcula exactamente más adelante. 

Esta es una forma rápida de hacer una regresión con una variable independiente, pero solamente aporta una fracción de la información relevante para hacer una regresión. Con el paquete de análisis de datos es posible calcular todos los elementos de una regresión, y es lo que veremos a continuación. 

Regresión lineal en Excel: el caso general

Para realizar una regresión lineal en Excel, primero necesitas primero instalar un complemento que te lo permita. 

Instalando el paquete de análisis de datos

Paso 1: En la barra de herramientas, haz click en “Archivo” y luego en “Opciones” (en la esquina inferior izquierda). 

Paso 2: En la nueva ventana de opciones, debes seleccionar “Complementos”. En la sección “Administrar”, selecciona “Complementos de Excel” y luego haz click en “Ir”.

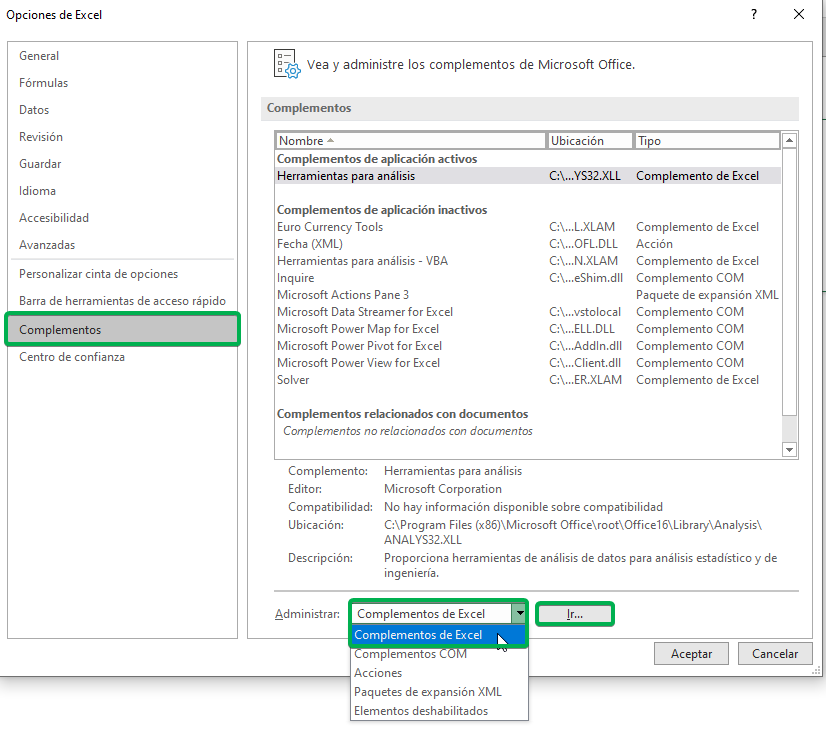
Paso 3: Aparecerá una nueva ventana, en la que debes verificar “Herramientas para análisis” y luego hacer click en “Aceptar”.

Si te diriges a la pestaña “Datos” de la barra de herramientas, verás que se ha agregado una nueva sección llamada “Análisis”, la que incluye la herramienta de “Análisis de datos”. 

Calculando una regresión lineal 

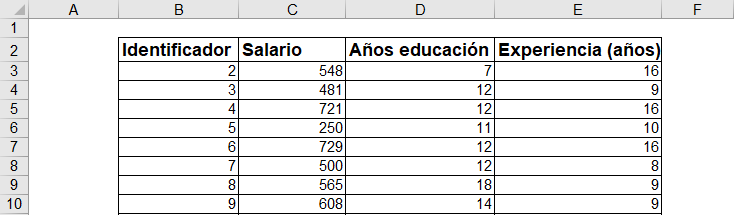
La siguiente tabla contiene información sobre distintas personas: su salario, sus años de educación y su experiencia. Tal como la mayoría de las encuestas que recogen información de este tipo, la base de datos no contiene nombres sino que un identificador numérico único para el individuo. 

Paso 1: Dirígete a la pestaña “Datos” y haz click en la nueva herramienta “Análisis de datos”. 

Verás que aparecerá una nueva ventana que deberás rellenar con la información pedida. 

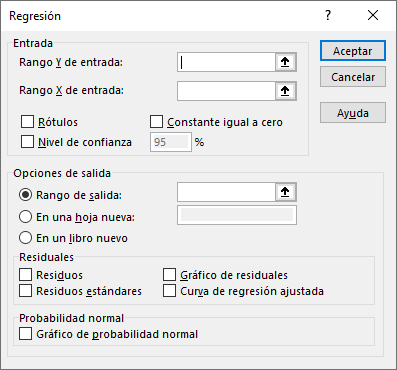
Paso 2: En “Rango Y de entrada:”, selecciona la columna que tiene información sobre la variable dependiente, en este caso, la de “Salario”. Tal como vimos en la fórmula genérica de una regresión, la variable independiente está denominada por una letra “Y”.  Fíjate bien de que estés seleccionando tan solo una columna con información. 

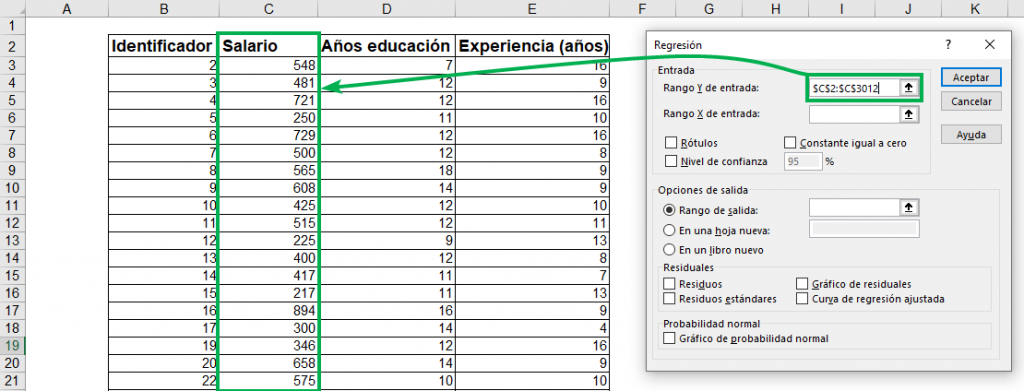
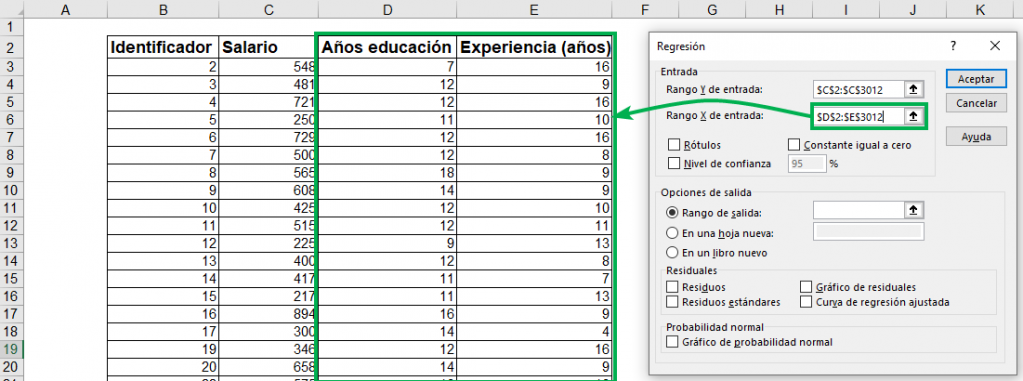
Paso 3: En “Rango X de entrada:”, selecciona todas las columnas que contengan información sobre las variables independientes. En este caso, las de “Años educación” y “Experiencia (años)”. En general, las variables independientes de una regresión se denotan por una “X”. Puedes seleccionar todas las columnas que quieras incorporar en tu análisis. En este caso son solo dos. 

Tip Ninja: Si las columnas están seperadas entre si, puedes seleccionarlas con el mouse apretando al mismo tiempo la tecla Ctrl. 

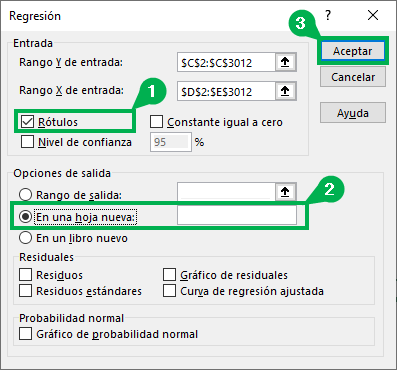
Paso 4: Selecciona el resto de las opciones que quieras incorporar en los resultados. Para este caso simple, tendremos que seleccionar la casilla de “Rótulos” puesto que las columnas seleccionadas tienen los títulos. Además, para “Opciones de salida”, selecciona “En una hoja nueva”. Más adelante veremos algunas de las restantes opciones de la planilla. Por ahora, solo presiona “Aceptar”. 

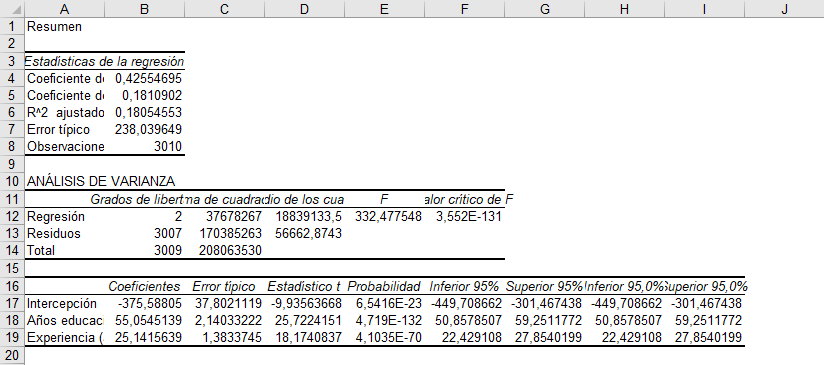
El resultado es el siguiente:

Interpretando los resultados de una regresión lineal con Excel

Ahora repasaremos los elementos más importantes de las distintas tablas de resultados de la regresión. 

Estadísticas de la regresión

Esta primera tabla incluye información sobre la regresión en general y no cada uno de sus elementos.

Para entender mejor, usaremos el siguiente gráfico que muestra la relación entre el salario y la educación, y la línea corresponde a la regresión lineal que se hace sobre los datos. 

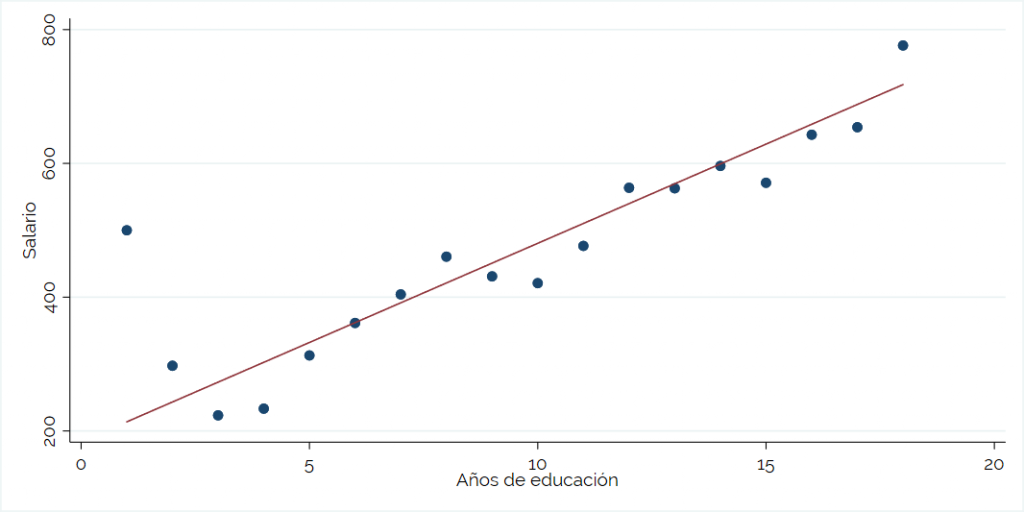
• Coeficiente de correlación múltiple: Es una medida de qué tan juntas se mueven las variables de la regresión. Va entre -1 y 1. Si el valor es cercano a 1, significa que las variables se mueven de manera similar. Si el valor es cercano a -1, significa que las variables se mueven de manera opuesta. Si el valor es cero, significa que no hay relación alguna entre las variables. En este caso, la correlación es de 0,426 (aproximado), con lo que las variables se mueven en el mismo sentido. Considerando la forma simplificada en el gráfico, que considera solamente la relación entre el salario y los años de educación, significa que la pendiente será positiva. 
• Coeficiente de determinación R^2: Esta es una medida mucho más usada e indica qué tan bien se ajusta el modelo. En palabras más simples, significa qué tanto explican la educación y la experiencia, en conjunto, lo que ocurre en el salario. Su valor va entre 0 y 1, y mientras más cercano a 1, las variables independientes explican una mayor cantidad de la variación de la variable dependiente. En este caso el R^2 es más o menos bajo, de 0,181. Esto se puede deber a que faltan otras variables que inciden en el salario de una persona, como puede ser la habilidad, la industria o el sexo. 
• R^2 ajustado: Tal como indica su nombre, es similar al R^2 pero este ajusta por la cantidad de variables que tiene la regresión. Esto ocurre porque si se agregan la suficiente cantidad de variables al modelo, entonces el R^2 se acercará cada vez más a 1, aun cuando esas variables sean casi totalmente irrelevantes. Luego, el R^2 “castiga” por la cantidad de variables que tiene la regresión, siendo una medida más estricta de qué tan bueno está el modelo. En este caso, es casi igual que el R^2 ya que el modelo tiene tan solo dos variables dependientes. 
• Error típico: También se le conoce como error estándar y corresponde a cuanto se desvían las variables de la predicción que realiza la regresión. Para verlo más fácilmente, es la distancia que tienen los puntitos (que son las observaciones) a la recta de la regresión. 
• Observaciones: Simplemente, la cantidad de filas que tiene la planilla con datos. 

Análisis de Varianza 

La segunda tabla de resultados de regresión, también conocida como tabla ANOVA (por su nombre en inglés, Analysis of Variance), contiene los elementos que analizan la variación de la regresión, tal como indica su nombre. Es decir, indica qué tanto se alejan los datos de la estimación.

En este caso, solo interpretaremos el resultado del estadístico F, que es igual a 332,47. Este estadístico indica si todos los coeficientes de la regresión, conjuntamente, son distintos de cero. Es decir, indica si el coeficiente que acompaña a “Años de educación” Y el coeficiente que acompaña a “Años de experiencia” son distintos de cero, que es lo mismo que decir que son conjuntamente significativos. En general, queremos que el estadístico F sea lo más grande posible, o también que el “Valor crítico de F” sea lo más pequeño posible. En este caso, tenemos que el estadístico F es 332,48 y que su valor crítico es prácticamente cero, por lo que sí podemos decir que los coeficientes son conjuntamente significativos.

Coeficientes

Esta tabla contiene lo que parece un montón de información, pero en realidad contiene la estimación puntual de los coeficientes y su significancia escrita de distintas formas. Vamos paso a paso. 

La columna coeficientes indica la estimación de los números que acompañan a la regresión. La forma general se escribiría: 

La interpretación de cada uno es la siguiente: 

• Intercepción: indica cuál es la estimación de la variable independiente cuando todas las otras variables son iguales a cero. En este caso, si una persona tiene cero años de educación y cero años de experiencia, entonces se estima que su salario sería de -375,59. Aunque este número puede no tener un sentido práctico, es clave entender su significado en una regresión. 
• Coeficiente de “Años de educación”: este coeficiente indica que, por cada año adicional de educación, el salario aumenta en 55,05 unidades.
• Coeficiente de “Experiencia (años)”: similar al anterior, este coeficiente indica que, por cada año adicional de experiencia, el salaio aumenta en 25,24 unidades. 

Tip Ninja: El salario puede estar en distintas unidades dependiendo del país de donde se obtuvo la información, como dólares o pesos. Si fueran pesos, entonces el coeficiente de educación se interpreta como que “cada año adicional de educación, aumenta el salario en 55,05 pesos”. Asegúrate de saber las unidades de todas tus variables para hacer una interpretación correcta.

Significancia de los coeficientes

La palabra significancia la encontrarás de manera recurrente en cualquier artículo que hable sobre regresiones. Ella se refiere a con qué tanta certeza podemos decir que el coeficiente que estimamos es distinto de cero. Por ejemplo, si decimos “el coeficiente que acompaña a educación es significativo”, entonces eso quiere decir que estamos bastante seguros que ese coeficiente es distinto de cero. Esto va más allá de la estimación puntual de los coeficientes (que acabamos de ver justo arriba), sino que tiene que ver con las distintas medidas que veremos a continuación. 

• Error típico: este error indica la variación que tiene la estimación del coeficiente. Será muy importante al momento de determinar la significancia. 

• Estadístico t: es el resultado de la división entre el coeficiente y su error estándar. Es una de las medidas de significancia de los coeficientes. Buscamos estadísticos t que sean grandes en valor absoluto, es decir, muy positivos o muy negativos. Con un estadístico t grande (en general mayor a 2), podemos decir que el coeficiente estimado es distinto de cero, es decir, que es significativo. 

• Probabilidad: más conocido como valor-p, es la probabilidad de que el coeficiente sea igual a cero. En general, queremos que el valor-p sea lo más pequeño posible, específicamente menor a 0,05. En nuestro caso, todos los valores-p de los coeficientes de la regresión son muy cercanos a cero, por lo que, nuevamente, podemos decir que son distintos de cero. 

• Las columnas “Inferior 95%” y “Superior 95% corresponden a los intervalos de confianza de los coeficientes. Es decir, dada la estimación puntual y su error típico, el coeficiente se mueve entre esos dos valores. Por ejemplo, podemos decir que el coeficiente de años de educación se mueve entre 50,85 y 59,25. Vemos que ninguno de los intervalos de confianza incluye el cero puesto que, como habíamos dicho anteriormente, rechazamos para todos los coeficientes, que estos sean iguales a cero. 

Tip Ninja: Puede que la estimación de un coeficiente sea distinta de cero, y al mismo tiempo puede ocurrir que ese coeficiente sea no significativo. Por ejemplo, considera el caso de que el coeficiente de educación es 55,05 (igual al que obtuvimos), pero es tan incierta su estimación, que su error típico es muy grande. Es tan grande, que produce estadísticos t menores a 2, valores-p mayores a 0,05, e intervalos de confianza que sí incluyen el cero. Asegúrate de siempre analizar estos valores al momento de realizar una regresión. 

Analizando los residuos de una regresión

La forma general de la regresión lineal contiene un elemento que aún no hemos considerado: los residuos. Estos corresponden a la diferencia entre el valor real de la variable independiente, y el estimado por la regresión. 

Supongamos la primera observación de la tabla, un individuo con 584 de salario, 7 años de educación y 16 años de experiencia. Dados los coeficientes de la regresión lineal, se estimaría que un individuo con esos años de educación y de experiencia tendría 412,06, que proviene del siguiente cálculo: 

Como bien te darás cuenta, existe una diferencia entre el salario efectivo del individuo y lo que la regresión estimó: 584 – 412,06=135,94. A esta diferencia se le llama residuo, y hay uno para cada una de las observaciones. Puedes obtener esta estimación con los elementos adicionales de la ventana para realizar una regresión en Excel. 

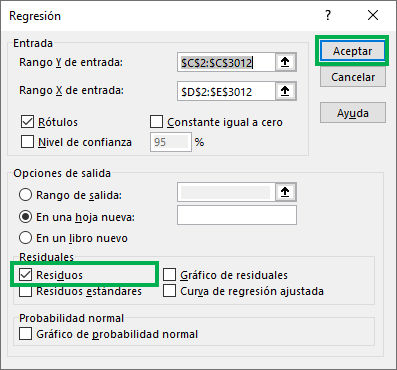
Paso 1: Considera nuevamente la ventana en la que se rellenan los datos de la regresión. Selecciona la casilla de “Residuos” y luego dale a “Aceptar” 

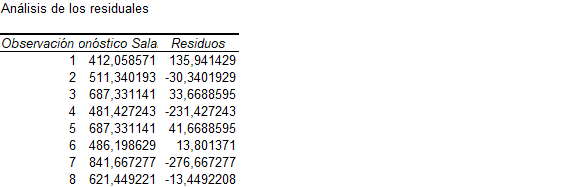
¡Y listo! Ahora la nueva hoja contiene el resultado de la regresión, pero además una nueva tabla de “Análisis de los residuales” que contiene la observación, el pronóstico del salario según los coeficientes, y el valor del residuo. 

Ahora ya tienes todos los elementos básicos para hacer una regresión e interpretar su resultado.